ヘロンの公式公式ヘロンの公式 3辺の長さがそれぞれ, , であるような三角形の面積は次の式で求まる但し, とする ヘロンの公式は, 三角形の3辺の長さが分かっているときにその面積を求めるための公式です 実際に計算してみると分かるのですが, 3辺の長さがすべて有理数の場合は計算が楽三角形の面積の公式 S = 1 2 a b sin C S=\dfrac{1}{2}ab\sin C S = 2 1 ab sin C において角度の情報を消すと有用な公式 S = a b c 4 R S=\dfrac{abc}{4R} S = 4 R ab c が得られる。→外接円の半径と三角形の面積三角関数(さんかくかんすう、英 trigonometric function )とは、平面三角法における、角の大きさと線分の長さの関係を記述する関数の族および、それらを拡張して得られる関数の総称である。 鋭角を扱う場合、三角関数の値は対応する直角三角形の二辺の長さの比(三角比)である。

如何计算等腰三角形的面积 包含图片
三角形 面積 sin なぜ
三角形 面積 sin なぜ-三角形の面積の求め方 sin, サイン(sin)を使った三角形の面積を求める公式とその証 ☺ そこで,下の図のように,三角形のうち,2辺と,その2辺がはさむ角と覚えておきましょう。 その工夫の仕方を覚えておきましょう。 12四辺形の面積を求めるヘロンの公式,チェバの 定理,メネラウスの定理を導く。 L オイラーは三角形の性質についての研究 (l 765)において三角形の垂心,重心,内心,外 心の座標を計算している。そして,外心,璽心,




直角三角形 维基百科 自由的百科全书
三角形の面積公式の証明1 サラスの公式 で紹介した「直交座標における三角形の面積公式」を認めてしまえば,証明は簡単です。 証明 A ( a b i), B ( c d i) A (abi), B (cdi) A(a bi),B(c di) とすると直交座標では A ( a, b), B ( c, d) A (a,b), B (c,d) A(a,b),B(c,d) となる三角形,又稱三邊形,是由三条线段顺次首尾相连,或不共線的三點兩兩連接,所组成的一个闭合的平面图形,是最基本和最少邊的多边形。 一般用大写英语字母 、 和 为三角形的顶点标号;用小写英语字母 、 和 表示边;用 、 和 給角標號,又或者以 這樣的顶点标号来表示。辺aと辺bの間の角を角Cとすると、三角形の面積は「ab sinC」なので、この公式を2回(分割してできた2つの三角形それぞれで)使うと、四角形全体の面積が分かります。 公式にすると以下のとおりです。 「面積= 05 辺 1 × 辺 4 × sin (辺1と4の間の角) 05 × 辺
三角形の面積は、その3つの辺が占める合計スペースです。 その面積を計算するための基本的な式は、三角形の底辺と高さに等しくなります。 高さと底辺による三角形の面積 Triangle area = (height * base) / 2 三角形の面積は、三角形の角度と長さを使用して 三角形面积=邻边×邻边×2邻边夹角的正弦 S=1/2absinC S=1/2acsinB S=1/2bcsinA面積= = 面 積 = 10 × 3 ÷ 2 = 15 面積= = 面 積 = 5 × 6 ÷ 2 = 15 答: 平方公尺。 答 : 15 平 方 公 尺 。 由例 可以知道計算三角形面積時,可以任選一邊的底和高,都可以算出一樣的答案。 由 例 2 可 以 知 道 計 算 三 角 形 面 積 時 , 可 以 任 選
Q abc の面積 s は で与えられるというのは,三角形の(2)2辺 角の場合の公式ですが,(1)3辺(3)2角 辺の場合に相当する公式はあるのですか。 a 三角形の形状について,(1)(3)の場合も残りのものが決まることを発展のところで確かめたので,面積を表す式もありそうです。この定理より,三角形の2辺の長さとその2辺が成す内角の大きさとからその三角 形の面積を計算できます. 例 平面上の相異なる3点A, B,C を頂 A B C 5 150 7 点とする三角形ABC において,AB=5 かつ BC=7 かつ 6 ABC=150 と する. sin150 = sin(60 90 ) = cos60 = 1 2 定理67より概要 ブラーマグプタの公式は、7世紀にインドの数学者 ブラーマグプタがヘロンの公式の一般化として得た定理である。 ヘロンの公式は三角形の3辺の長さから三角形の面積を求める公式であるが、ブラーマグプタの公式は四角形の 4辺の長さから四角形の面積を求める公式である。



高中数学牛x 公式 利用平面向量快速求三角形面积 1 努力学习网



少有人走的路 三角函数超入门 4 钝角三角比 三角形面积
より一般に、内接円を持つ四角形 abcd の面積は、 = とおくと次で与えられる。 S = √ abcd sin t 双心四角形に対する公式は、 t = π/2 という特殊な場合である。$3$ 辺の長さと面積がすべて整数であるような三角形を「ヘロンの三角形」(Heronian triangle)と呼ぶ「ピタゴラスの三角形」(各辺の長さがすべて整数であるような直角三角形)は「ヘロンの三角形」であるよって, $1$ 組の辺の長さが等しい $2$ つの「ピタゴラスの三角形」の等辺を貼り合わせたり例子:这个三角形的面积是多少? (注意:12 是 高,不是左边的长度) 高 = h = 12 底 = b = 面积 = ½ bh = ½ × × 12 = 1
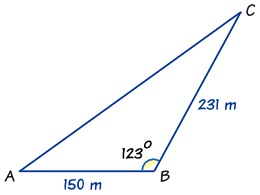



非直角三角形的面积




11 三角面積524 已知一三角形的三高長為1 3 1 5 1 7 求此三角形的面積 99 萬芳高中 答解 令三邊長為3t 5t 7t 則 T 2
三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する このページは、このような人へ向けた内容となっています 三角比を使った三角形の面積の求め方を知りたい 三角比の公式は知っているが使い方がわからない 三角形の面積を求めるための、色々な方法を知りたい 三角比(\\(\\sin, \\cos, \\tan\\))を使った三角形の面積を求める方法はいく三角形の2辺と角度(°)を入力 辺 a = 3 辺 b = 4 角度(°)= 30 面積 S = 3000 三角形の2辺と角度(°)を入力 辺 a = 54 辺 b = 126 角度(°)= 58 面積 S = 251 このように三角形の面積を計算してみました。 その他のサンプルプログラムも合わせてご覧ください




三角形面積公式 三角形面積公式是指使用算式計算出三角形的面積 同一平面內 百科知識中文網




高校数学 3辺 三角形の面積 を求める方法 練習編 映像授業のtry It トライイット
二等辺三角形(二つの合同な辺を持つ三角形)において、合同でない辺を底辺として持つ頂垂線は、その辺の中点を足に持つ。 また合同でない辺を底辺とする頂垂線は、その頂角の二等分線である。 頂垂線またはその長さを表すのにしばしば文字 h (height に由来) が用いられ、対応する頂点を三角形の面積(2辺と夾角から) 110 /11件 表示件数 5 10 30 50 100 0 1 2129 男 / 60歳以上 / エンジニア / 役に立った / 使用目的 三角形の面積計算(年前エクセルで自分で作ったもの)検証として ご意見・ご感想 EXCELLで三角形の面積(3つの方法三角形の外接円の半径、内接円の半径と面積の関係 S=1/2r(abc) 三角形の頂角の二等分線の長さ:基本2パターン、裏技公式 x=√(abcd) とその証明



所有類別 我的m讚




高中數學 三角函數 正弦定理與餘弦定理 1 三角形面積公式 吳汀菱 Youtube
中心を O とします。 すると、 ∠COA = 2θ ∠ C O A = 2 θ となりますね。 また、 C から AB に下した垂線の足を D とします。 この三角形の面積を出すときに、 AB = 2 A B = 2 を底辺だと考えると、高さは CD = CO × sin2θ C D = C O × sinいろいろな図形上の面積分 = 1 0 1y 0 f (x, y)dxdy T f dS = 1 0 1x 0 f (x, y)dydx y 1 y x y 1 1 0 x 1 x T x y 1 1 0 T 例.三角形 T = {(x, y) x y 1, x, y ⇥ 0} 上の積分 面積分 f dS の計算は適当な座標軸に沿った2回の積分を実行 することによって行う.本時の目標 まず,鋭角について三角比(三角関数)の定義を確認し, \(30°\) , \(45°\) , \(60°\) の三角比を答えることができる。 三角比を簡単な計測に活用する。 \(0°\) から \(360°\) の角について,円を用いて三角関数の定義を拡張し,新たな定義を理解する。



三角函数 玄数
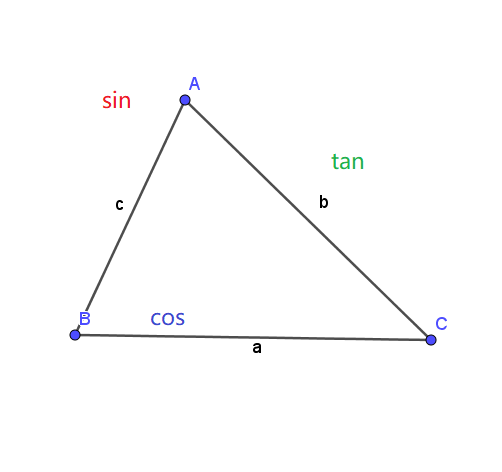



三角形中三角比的特殊公式 知乎
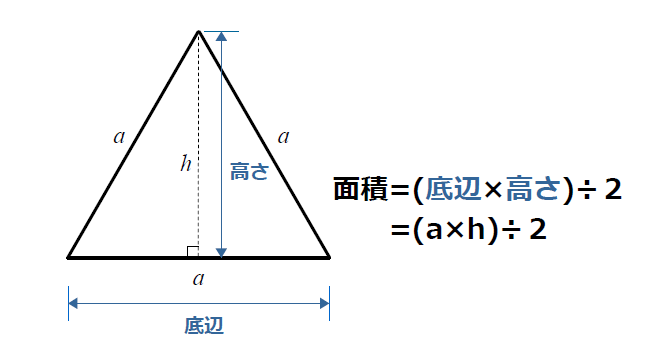
三角形の面積(1辺と2角から) 計算は正しいみたいですが、表示しているhの式が間違っています。 h=S/ (a/2) なので、h=の式の分子分母ともにtanでなくsinです。 あとせっかくなのでLの表式にhを使わず、正弦定理から導かれる式L=a (1 sinα/sin (αβ) sinβ/sin三角形の面積の公式の確認 三角形 O A B OAB O A B において, ∠ A O B = θ \angle AOB = \theta ∠ A OB = θ とすると,三角形 O A B OAB O A B の面積 S S S は, S = 1 2 ∥ a undefined ∥ ∥ b undefined ∥ sin θ S = \dfrac{1}{2}\\overrightarrow{a}\\\overrightarrow{b}\\sin\theta S = 2 1 ∥ a ∥∥ bここまでで用いた法則や計算方法を踏まえ、特殊な値を用いたり三角法を元に単純化したりせずとも、下記のような公式で二等辺三角形の面積が求めらえることが分かります。 A = 1 2 s 2 s i n θ {\displaystyle A= {\frac {1} {2}}s^ {2}sin\theta } 「s」は二つの等しい辺を




高二高中數學的 高二數學 三角形面積公式3 6 充實版 筆記 Clear




三角形邊長面積四邊形的面積 Duph
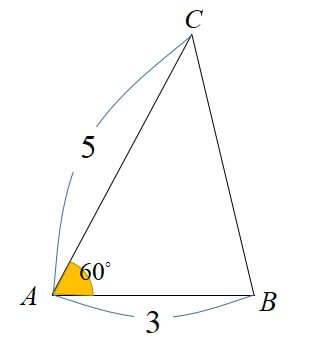
三角形の3辺が与えられたときの面積の求め方 「3辺の長さが,5,4,7の三角形の面積を求めよ。 」という問題がわかりません。 面積を求めるときは,公式 S=1/2 bc sin A に当てはめればいいことは知っています。 しかし,この公式を使うには, A の大きさればどのような三角形か求めよ. (Hint 半径1 の円に内接する三角形の3 つの角の大きさをそれぞれx,y,π−x−y (0 < x < π, 0 < y < π,0 < x y < π) とするとき,その三角形の面積は2sinx siny sin(π − x − y) = 2sinx siny sin(x y) で与えられる(正弦定理のちょっとその面積の半分が \vec a,\vec b,\vec c a,b,c によって表される三角形の面積となります。




直角三角形 维基百科 自由的百科全书



Q Tbn And9gcs4mf4ga4ivcw9oaofx1 Zkqgkhy6m1tx85ng7ya0kcksl0rfiq Usqp Cau




三角形的面积公式小学



三角形面积公式sin 冷知识 球面三角形面积是怎样求出来 尚书坊




三角形abc之中線長為4 5 6 求三角形面積 信欣茗數學園地 隨意窩xuite日誌



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典



三角形面积的计算公式 信息阅读欣赏 信息村 K0w0m Com




三角形的五心 維基教科書 自由的教學讀本



三角形的面积公式 腾讯视频
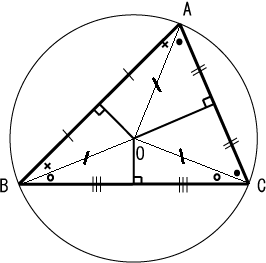



外接圓 維基百科 自由的百科全書




サイン Sin を使った三角形の面積を求める公式とその証明 数学i By ふぇるまー マナペディア




4种方法来计算三角形面积
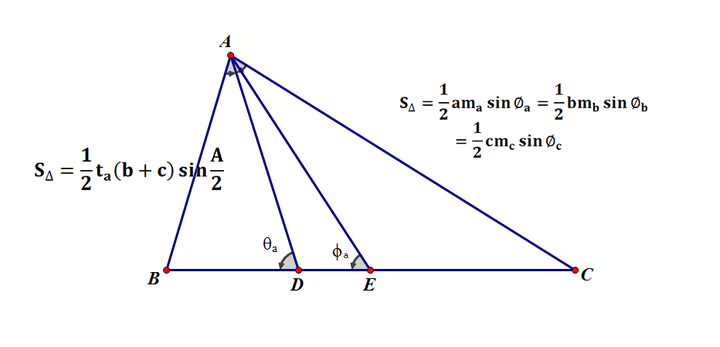



三角形的面积公式七叙 知乎




如何计算等腰三角形的面积 包含图片



用sin求三角形面积 西瓜视频搜索



1



数理之路 三角形面积公式以及三角函数正弦和角公式 腾讯新闻



トップ100 正三角形面積小学生 最高のカラーリングのアイデア



Q Tbn And9gct1v2pgvk7whjg1d4uotovbnlacdz8gujsvt8mxujwvqowjyn6w Usqp Cau




正三角形高面積正三角形 Qmog Fi



三角形面积公式sin 万图壁纸网




淺談 三角形面積公式 Hackmd
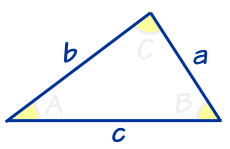



非直角三角形的面积




數學競賽中的面積問題與面積方法 一 每日頭條



用sin求三角形面积 西瓜视频搜索




那些你不知道的技巧 四邊形分割後面積計算 Dsemathinfo




三角形的面積




求三角形面積問題 這個公式還是非常好用的 每日頭條




一些有关三角形面积推论及展开 哔哩哔哩
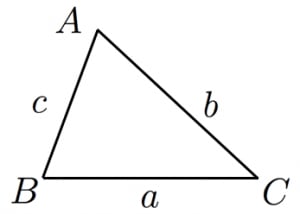



Sinを用いた三角形の面積公式 高校数学の美しい物語




設 三角形abc 三內角與三邊長有 B C Cos 2a os 2b Ccos 2c的關係 證 三角形abc 為 角b 角c 的等腰三角形 或 角a 1度的三角形




计算五边形的面积 建议 August 21



三角形面积用sin表示 三角形的面积公式sin 三角形面积怎么算




正三角形面積公式證明從三角形的面積談起 Mrsysy




三角形的面積



數學 高二上三角函數公式 小編過路君子




正弦区域高度面积公式的三角形律png图片素材免费下载 图片编号 Png素材网



正弦定理求三角形面积 万图壁纸网




高校 数学i 図形と計量 三角形の面積sinの利用 Youtube




3 10 三角形面積公式的推導 Youtube



用sin求三角形面积 西瓜视频搜索



Q Tbn And9gcr7w5872uyvmvig8vf1xeyoxmjhhoh Safltyblfewvm9f Tlta Usqp Cau




三角形的面積



Sin サイン を用いる三角形の面積公式を解説




宇宙數學教室 日本數學奧林匹亞jmo 1991 初賽 問題3 給定三角形三中線長度 求三角形面積




三角形の面積を求める公式7選 高校数学のまとめにどうぞ



三角形的面积公式十叙 知乎



四邊形面積 Wonder Math



正三角形の面積計算 ゆるゆるプログラミング




三角形面積公式 兩邊一夾角 Youtube




淺談 三角形面積公式 Hackmd




4种方法来求四边形的面积
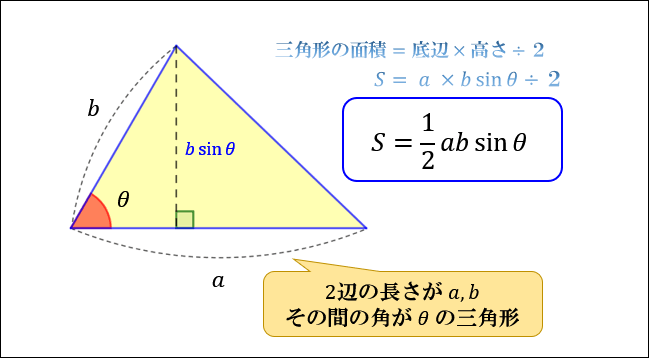



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



三角形面积公式梯形 万图壁纸网




為什麼aob面積要乘以sin1度 Clear



三角形的面积公式 万图壁纸网




三角形面積公式sin 三角形面積公式 Duph




衝刺18年高考數學 典型例題分析23 餘弦定理和正弦定理 壹讀



少有人走的路 三角函数超入门 4 钝角三角比 三角形面积




三角形的面積




三角形面積公式1 2 Sina Geogebra




三角形面积怎么求



等边三角形面积如何计算等边三角形面积怎么计算




Gd 4af 8求平行四邊形abcd的面積 信欣茗數學園地 隨意窩xuite日誌



三角形面积计算公式 三角形面积计算的万能公式 最全知识分享



用向量算面積 老王的夢田 痞客邦




高校数 三角比 三角形の面積 2辺とsinから オンライン無料塾 ターンナップ Youtube



用sin求三角形面积 西瓜视频搜索




Amc系列 第一講 數學中的面積公式都是怎麼來的 每日頭條




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト
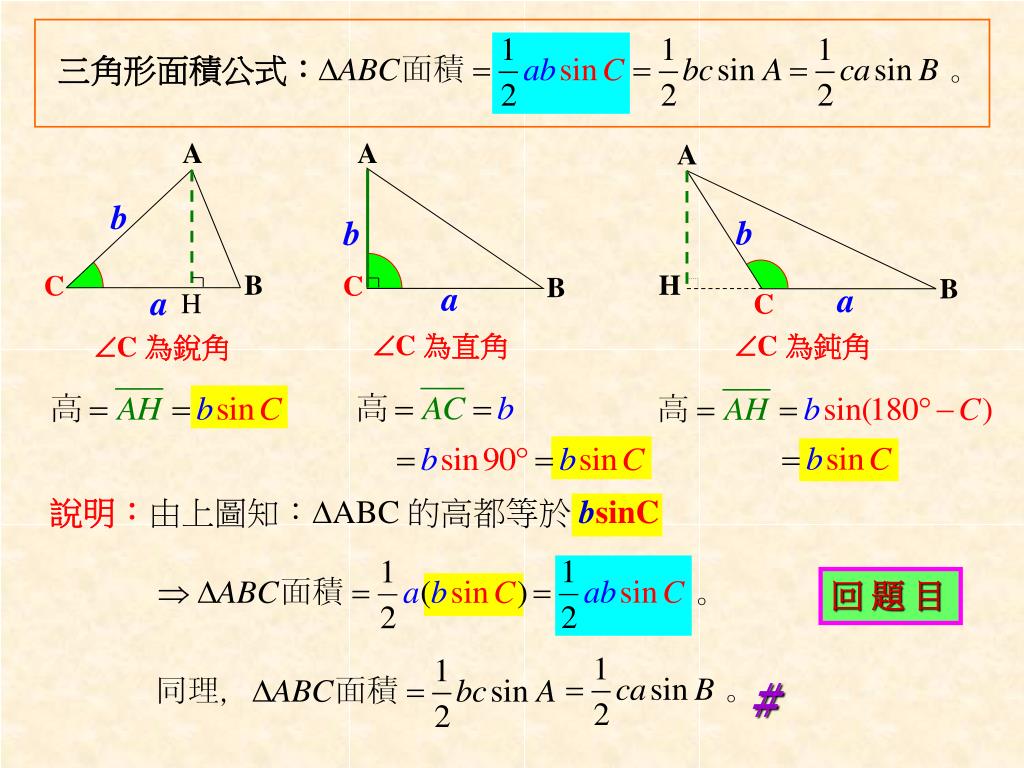



Ppt 重點一 銳角 廣義角的三角函數powerpoint Presentation Id




淺談 三角形面積公式 Hackmd



三角函数求三角形面积 信息评鉴中心 酷米资讯 Kumizx Com



三角形面积推导图片 信息评鉴中心 酷米资讯 Kumizx Com
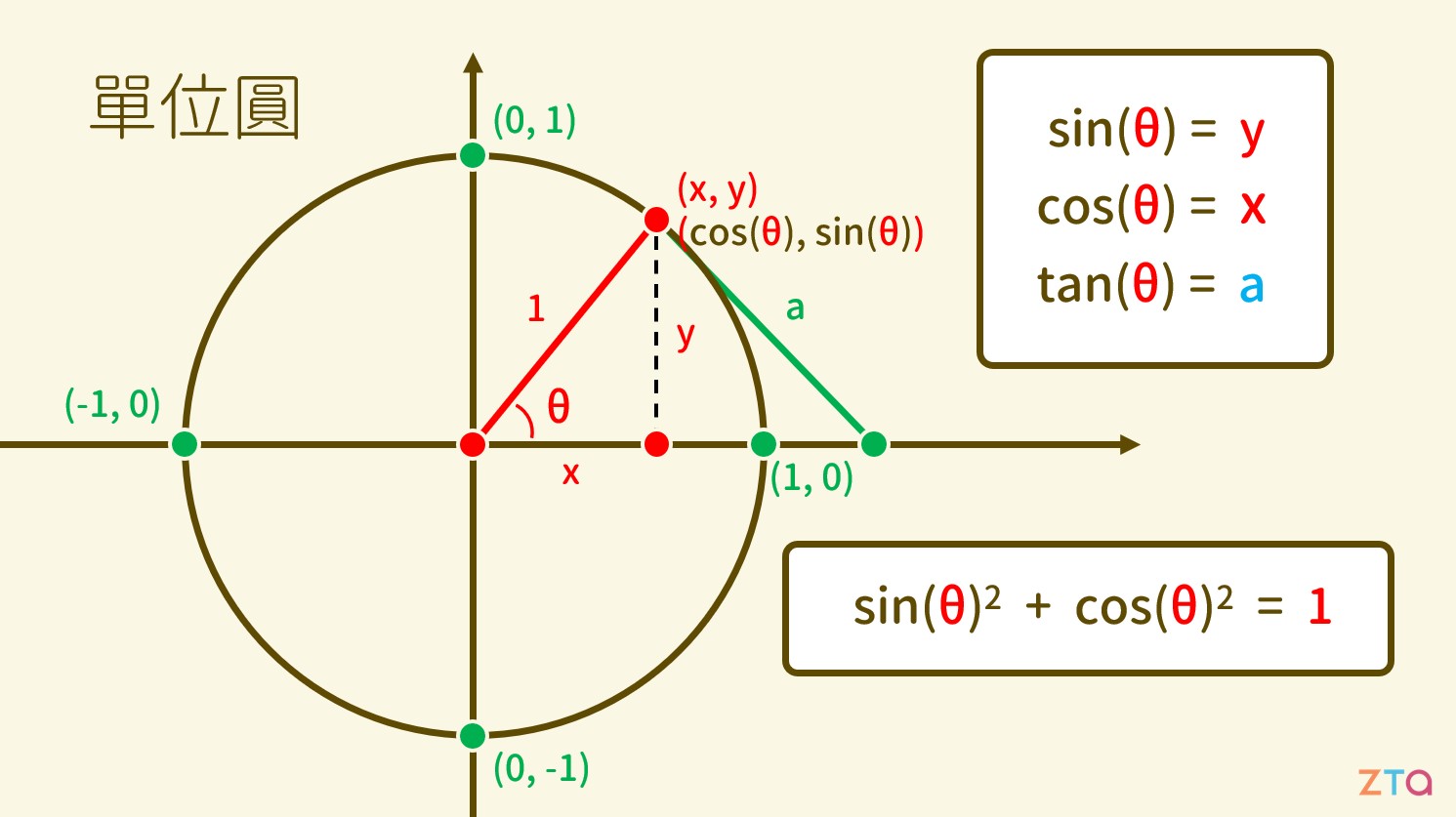



三角函數公式整理 學呀 基礎數學 數學 Sin Cos Tan 單位圓




直角三角形公式面積 直角三角形的面積公式是什么 作業幫 Jvvx




三角形的面積




若三角形三邊長分別為 2 5 7 求此三角形面積 Clear



数理之路 三角形面积公式以及三角函数正弦和角公式 腾讯新闻




Sin Cos Tan 系列3 求三角形面積嘅時候用底乘高除二大家就聽得多啦 但係如果用另一條公式用sin大家又聽過未呢




三角形面积公式sin计算公式推导过程详解说明 小街网




程俊老師 三角形面積公式整理 Facebook
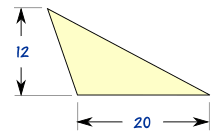



非直角三角形的面积




怎样在非直角三角形中用sin或cos 雨露学习互助




怎么计算三角形面积 生活百科




教學0 5absinc Heron Formula Sine Cosine Formula 三角形面積公式 希羅公式 正弦及餘弦定理 Youtube
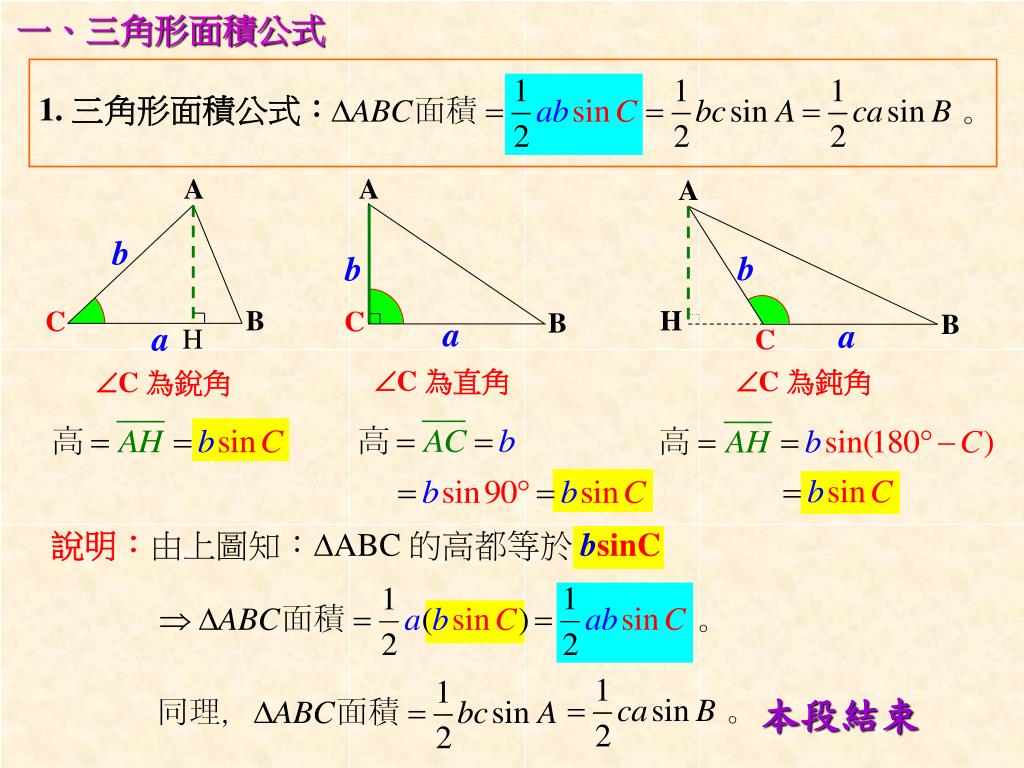



Ppt C 為直角powerpoint Presentation Free Download Id



三角形心系列 外心篇 三角形外心及其面积公式 哔哩哔哩 つロ干杯 Bilibili



三角函数 玄数




三角形公式面積三角形面積公式 Utvos



少有人走的路 三角函数超入门 4 钝角三角比 三角形面积




三角形面積公式小學 小學三角形的面積公式 作業幫 Gkgnae



0 件のコメント:
コメントを投稿