(1) 対角行列の対角要素は固有値そのものであることから,q>0 であれば正 定,qï0 であれば準正定,q4 のとき行列Qは正定となる。 この定理はアーサー・ケーリーとウィリアム・ローワン・ハミルトンという2人の人物の名前にちなんでいます。「正方行列 A に対して、det(AλE) という多項式の λ の部分を A に変えたものは零行列になる。」という定理です。この定理の利点は、①次数を下げること② n乗の計算ができる線形代数学講義ノート まえがき これは大学1 年次を対象にした線形代数学の講義ノートである 前半部分では連立1 次方程式の解法 と行列式の計算を主に扱う 後半は線形空間の抽象論の初歩を踏まえた上で, 行列の対角化までを目標に 定めている

三角形行列式计算证明 见下图 有关反上三角行列式的证明问题 三人行教育网 Www 3rxing Org
数学 行列 証明問題
数学 行列 証明問題-対称行列と交代行列問題と証明 この記事では, 対称行列と交代行列について次の性質を証明します。 性質を証明する前に, 対称行列と交代行列の定義をそれぞれ確認しておきます。 正方行列 A A が tA= A t A = A を満たすとき, A A を 対称行列 という高校数学の基本問題 Gogle site →数ⅠA →数ⅡB →数Ⅲ (旧C) ***最近の更新*** 約数の個数,約数の総和 確率の入試問題 確率の漸化式(入試問題) 反復試行の確率(入試問題) 絶対値付き関数の定積分 Rの関数hist




线性代数的一个小问题 行列式等于0 因为三次方矩阵的范围为2 365bet开户网站 Www 365 2 Com
次数の低下({ 行 or 列 }方向) { 行 or 列 } に対するその他の性質 同じ値を持つ { 行 or 列 } が複数存在すると行列式1gであることを,B のサ イズに関する帰納法により証明する.B のサイズが1ならば,これは成立する.B のサイ ズが2以上のとき,次の三つの場合に分けられる.定理 5 97 (エルミート行列の固有ベクトル) エルミート行列において, 異なる固有値に属する固有ベクトルは直交する. (証明) エルミート行列は正規行列であるので固有ベクトルは直交する. または,次のように示す. , , , () とする.
行列の積の行列式の定理の証明(2次の正方行列) 2次の 正方行列 A= (a11 a12 a21 a22),B =(b11 b12 b21 b22) A = ( a 11 a 12 a 21 a 22), B = ( b 11 b 12 b 21 b 22) の 行列の積 を考える. b1 = (b11 b12) b 1 = ( b 11 b 12) b2 = (b21 b22) b 2 = ( b 21 b 22) とおくと B= (b1 b2) B = ( b 1 b 2) と表わせる. 数学・算数 行列の証明問題です。 大学受験問題の参考書にのっているのですが、わかりません。よろしくお願いします。 この問題は、行列なので、行列の中は、(a,b,c,d)=(左上、右上、左下、右下 質問No 正則行列と逆行列 定義 正方行列 A が 正則行列 であるとは、 A B = B A = I となる正方行列 B が存在することをいう。 問題1(逆行列の一意性) 正方行列 A に対し、 A B = B A = I となる正方行列 B は存在すればただ一つ であることを示せ。
行列(線形写像)の階数 行列の列ベクトル(48ページ)による表示 例 A= 12 31 を2つの列ベクトルa1= 1 2 3,a2= 2 01 を考え、A = a 1 a2 と表すことがある。 この考えは一般のm 行n 列の行列でも使われる。 A= a11 a12 a1n a21 a22 a2n5 行列式 51 置換 nを自然数nとし,n個の文字1;2;線形代数問題集(0908) 3 行列と行列式 31 逆行列 1 次の行列に逆行列が存在するならばそれを求めよ。 (1) 12




行列式乘法规则的证明方法及其应用 豆知网




行列式证明二次曲线定点 值 问题 每日头条
7/1 第3回最短経路問題と動的計画法(DP) 7/8 第4回最適制御 7/18* 第5回二次計画法(QP)とモデル予測制御(MPC) 7/22 第6回凸解析と線形行列不等式 7/29 第7回線形行列不等式(LMI)による制御系解析・設計 8/5 第8回非線形最適化 * irregular目次 線形数学i 演習問題 第1 回 写像 1 線形数学i 演習問題 第2 回 平面ベクトル・空間ベクトル 5 線形数学i 演習問題 第3 回 行列の積 12 線形数学i 演習問題 第4 回 正方行列・1 次写像 21 線形数学i 演習問題 第5 回 連立1 次方程式 33 線形数学i 演習問題 第6 回 行列の基本変形 64 線形数学i 演習問題スライド 29 右辺中の行列式を 行で展開 スライド 30 場合2:一般の行の交換時 スライド 31 隣接する行の交換を繰り返し適用して、 望みの交換を実現する。



范德蒙行列式例题请教一个范德蒙的问题




線形代数の正則行列の証明問題です 上の4行が問題で それより下が私 数学 教えて Goo
;n を並べ替えたものであ る.したがって,Mn の置換全体の集合をSn とするある { 行 or 列 } と別の { 行 or 列 } とを入れ替えると行列式は反転;正則行列の証明問題 問題は「Aがm次正則行列、Dがn次正則行列ならばに二のm×n行列Cに対し次の行列X,Y,Zは正則であることを示せ。 またX^1,Y^1,Z^1を求めよ。 X= |A B| |0 D| Y= |A 0| |C D| Z= |B A| |D 0| 」 です。 証明は逆行列を求めて正則行列




行列式の証明問題 次の問題がどうしても解けません どなたか教えてください Okwave




下三角形行列式证明推导 技术成就梦想 梦想成就未来 Csdn博客 下三角行列式计算公式推导
行列式の計算の演習問題 12 問(解答付き)|線形代数学 N を非負整数全体の集合とする。 Sn を {1,,n} から {1,,n} への全単射全体とする(n 次対称群)。グラフ分割問題とコミュニティ検出 計算機科学の分野で,計算困難な問題は古くから研 究され,様々な発展を遂げてきました.グラフの分割 問題は,そのなかのひとつだと捉えることもできます. 由緒正しいグラフ分割は,入力として,全体をq個のモ狙い:計算問題だけでなく証明問題を出題してみた。 補足:教科書のp37, 問題4(3)。そこでは、定理241(p34)を使って証明しているが、その定 理は3章の内容を使う。上で与えた証明は定理241 を用いずに、逆行列の定義だけを用いて いる。




行列式 羊小羚 博客园




第二章行列式行列式的定义与性质行列式的计算cramer 法则解线性方程组的消元法消去法的应用 Ppt Download
入試問題の中から,特に押さえておきたい問題を中心に,基礎~標準問題をセレクトしています。 基礎・標準問題を しました。 問題と解説・講評はpdf形式で作成されています。Acrobat reader 40以降でご覧下さい。 pdfファイルは別ウィンドウで表示されます。;ng とする.写像 ˙ Mn!Mn が全単射であるとき,˙ をMn の置換といい, ˙ = 1 2 n ˙(1) ˙(2) ˙(n) と表す.˙(1);˙(2);;nからなる集合を Mn = f1;2;



行列式と行列 Determinant And Matrix




N 级行列式 一个大学狗的日常
熊本大学 大学教育統括管理運営機構附属 数理科学総合教育センター/Mathematical Science Education Center 〒 熊本市中央区黒髪2401 全学教育棟A棟3階 (数理科学総合教育センター事務室)て4 を採用し、証明している教科書もいくらかある。この定義の利点 は、最初から縦と横を区別していないことだろう。 • 標準形による証明。1,2,8,9 が等しいことが示される。ガウスの消去法 が理解できるなら、階段行列を使った証明法も理解できるだろう。問題1 連立一次方程式を解く問題 問題2 逆行列を求める問題 問題3 行列式を求める問題 この核心解説シリーズでは, 以下の内容を予定しています: vol 1 行列の基本変形のやり方 vol 2 基本変形の仕組み vol 3 連立一次方程式の解法 vol 4 逆行列の求め方




遞推公式法在行列式計算中的證明與應用 Getit01




线性代数论文 线性代数中行列式教学的思考 Doc 三九文库网
一般固有値問題から学ぶ線形代数 線形代数学において、線形空間、基底、行列の固有値問題から、さらに一般固有値問題、 ジョルダンの標準形まで講義をすすめることは難しく、理科系教養の講義でも線形代数の 一部の紹介で終わってしまうことが多い。代数学I 中間テスト予告問題 解答例(完全版) 担当 大矢浩徳(OYA Hironori)y 代数学I の成績は中間試験40 %、期末試験60 %の配分で付けられる 出席等は考慮されない 問題1 は必ず出題される その他、問題2{4 のうち1 問、問題5{6 のうち1 問が出題される 予告問題はこれで全てであるが、予告問題「線形代数」について、演習問題を解くことによって学ぶ。数学を学ぶすべての人に理解して欲しい内容である。 対象/前提 一般/「線形代数」の内容を理解していること キーワード ベクトル,行列,行列式,線形空間,線形写像,固有値,固有ベクトル,対角化




N 级行列式 一个大学狗的日常




行列式证明二次曲线定点 值 问题 每日头条
直交行列 4 問題5 1 行列式が1, −1の奇数次の直交行列はそれぞれ1, −1を固有値にもつことを示せ 2 A ∈ O(3)とする このとき, あるP ∈ O(3)およびθ ∈ 0,2π)が存在し, P−1AP = 0 B @ ±1 0 0 0 cosθ −sinθ 0 sinθ cosθ 1 C A となることを示せ転置行列 行列 Aの行と列を入れ替えて作られる行列をAの 転置行列 といい, A t と表す. A = ( a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ) のとき, A t = ( a 11 a 21 ⋯ a m 1 a 12 a 22 ⋯ a m 2 ⋮ ⋮ ⋱ ⋮ a 1 n a 2 n ⋯ a n m ) となる.例えば行列の性質を数学的帰納法で証明するときに活躍します( b b b が縦ベクトル, c c c が横ベクトルのとき, t t t のサイズは a a a のサイズより1大きいです,また d − c a − 1 b dca^{1}b d − c a − 1 b はスカラーとなり扱いやすいです)。




度证明行列式的有关性质 数学 Www Com



4月1日作业数值型行列式计算化成上三角 哔哩哔哩 つロ干杯 Bilibili
実数行列A 𝑎 𝑏 𝑏 𝑐 を考える。ただしa≠b,またはc≠dとする。 この時X= 𝑦 𝑥 に対してf(x)=tXAX=𝑎𝑥2 2𝑏𝑥𝑦 𝑐𝑦2 とおく。𝐴の固有値をλ1λ2とする時、以下の問に答えよ。 (1)λ1λ2は相違なる実数であることを示せ。 (2)λ1λ2に対する固有ベクトルをu1u2とする時、u直交行列の定義 n × n n\times n n × n の実正方行列 U U U に対して,以下の5つの条件は同値です。この条件のいずれか1つでも(従って全部)満たすとき U U U を直交行列と言います。 (同値であることの証明は記事末で)固有値と固有ベクトル 1 行列の固有値問題 n次正方行列A A = a11 ··a1n am1 ··amn について次の方程式を考える。 Ax = λx (1) ここで、x はn項列ベクトル、λは未知のスカラーパラメータである。 この形の方程式は、物理学、経済学、情報科学、など多くの分野に現れる重要な方程式であり、




2次正方行列の逆行列 その一般形 身勝手な主張




一类对称循环行列式的性质 参考网
問題 上の命題を証明せよ。 命題 任意の正方行列 は、適当な対称行列 と、交代行列 を用いて、 とただ一通りに表される。 問題 として、上の命題を検証せよ。 問題 次正方行列 を対称行列 と交代行列 の和に分解せよ. 問題 上の命題を証明せよ。(問題 次の等式を証明せよ 問題 微分可能な の関数 を要素とする 次正方行列 を考える その行列式 も の微分可13 外積(3次元実ベクトル) 定義13 2 つの3 次元実ベクトルa = 0 B @ a1 a2 a3 1 C A,b = 0 B @ b1 b2 b3 1 C Aに対して,その外積a×b を, a×b = 0 B @ a2b3 −a3b2 a3b1 −a1b3 a1b2 −a2b1 1 C




行列式を解く 10 問題11 齊藤数学教室 算数オリンピックから大学数学入門




反对角行列式公式 反对角行列式计算法则 反对角矩阵行列式
定理2 任意のグラフの接続行列は完全単模である. 証明:接続行列の任意の正方小行列B に対してdetB 2 f0;1; ある { 行 or 列 } に別の { 行 or 列 } の c 倍を加えると行列式は変化しない;問 2 60 (対角行列の可換性) 対角行列どうしの積は可換である.これを示せ. (証明) 対角行列は , と表わされる. これを用いて示す. 問 2 66 教科書(p10)問題 12




范德蒙德行列式怎么算 百度经验




四阶行列式计算 玩转线性代数 4 第三节 四阶行列式的讨论 Weixin 的博客 程序员宅基地 线性代数4阶行列式计算公式




行列式性质证明题 证明题行列式 三人行教育网 Www 3rxing Org




行列式乘法规则的证明方法及其应用 豆知网




行列の固有値は1以下だと証明する問題です Clear




若矩阵a可逆 则a的行列式不等于0 技术成就梦想 梦想成就未来 Csdn博客 A可逆a的行列式不等于0证明




考研数学复习资料




線形代数 解説 26 表現行列の考え Youtube



行列式証明問題です 方法がわかりません 右辺から左辺に変 Yahoo 知恵袋



行列式の問題です 証明が分かりません お願いします Yahoo 知恵袋




行列式 A B B A A B A B の証明 ばたぱら




线性代数的一个小问题 行列式等于0 因为三次方矩阵的范围为2 365bet开户网站 Www 365 2 Com




行列式恒等式的证明及其应用 百度经验



随伴行列の証明問題 行列a Bに対して Ab B A Yahoo 知恵袋




用向量法证明梅涅劳斯定理和塞瓦定理 百度经验




十一 用行列式速算空间法向量 三阶行列式求法向量 德涵网




行列式性质证明题 证明题行列式 三人行教育网 Www 3rxing Org



余子式 行列式按行 列 展开 玄数




反对称行列式怎么算 什么叫反对称行列式 求举例子 三人行教育网 Www 3rxing Org




正則行列の逆行列を求めてみよう 行列の基礎をふりかえる 身勝手な主張




线性代数 行列式 单元综合练习题及参考解答 网易订阅




四阶行列式计算 玩转线性代数 4 第三节 四阶行列式的讨论 Weixin 的博客 程序员宅基地 线性代数4阶行列式计算公式




递推公式法在行列式计算中的证明与应用 知乎
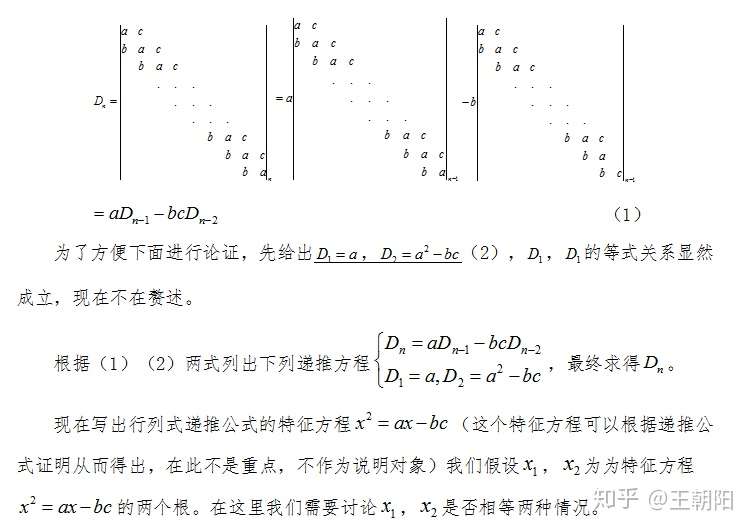



递推公式法在行列式计算中的证明与应用 知乎



正則行列と逆行列の理論の演習問題 18 問 解答付き 線形代数学 蛍雪に染まる




線形代数証明問題です 証明問題を解くことが出来ません 2aの問題なので Okwave




行列式を解く 19 問題24 25 齊藤数学教室 算数オリンピックから大学数学入門




6阶行列式中项a23a41a35a16a52a64的符号 雨露学习互助



行列式的性质 玄数




行列式函数问题 知乎
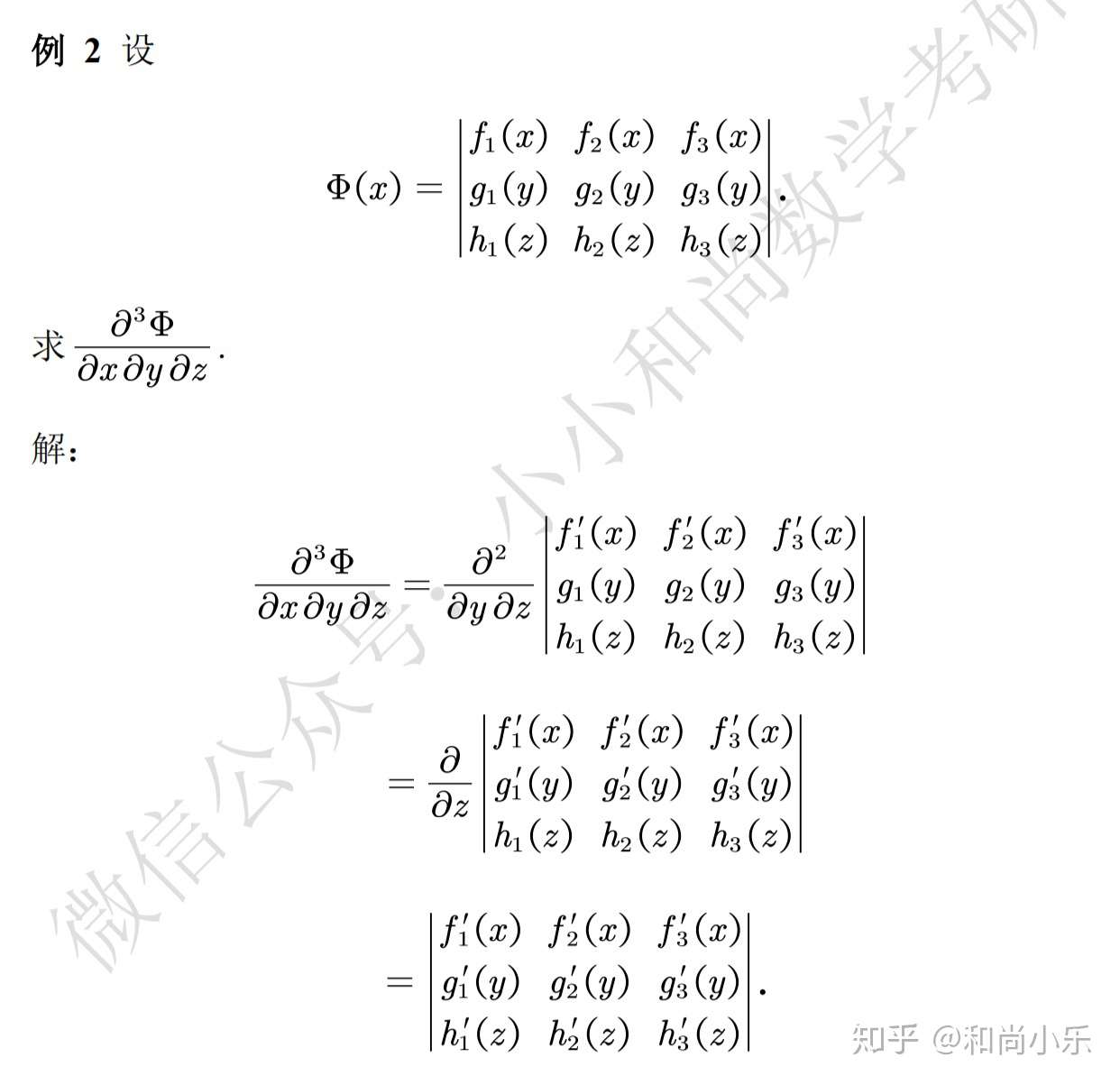



行列式函数问题 知乎




利用行列式性质证明下列等式 利用行列式的性质证明下列等式 三人行教育网 Www 3rxing Org




第二章行列式行列式的定义与性质行列式的计算cramer 法则解线性方程组的消元法消去法的应用 Ppt Download




行列式を解く 18 問題23 齊藤数学教室 算数オリンピックから大学数学入門



余子式 行列式按行 列 展开 玄数




行列式 証明 画像の行列式がa0x N A1x N 1 Anを示す問題で 数学 教えて Goo




行列式を解く 14 問題15 齊藤数学教室 算数オリンピックから大学数学入門




行列式の問題 Integers ニュートピ Twitterで話題のニュースをお届け




行列式函数问题 知乎



分块矩阵及其应用下载 Word模板 爱问共享资料




中值定理证明题中的 行列式问题 百度经验




方阵乘积的行列式等于各自行列式的乘积 技术成就梦想 梦想成就未来 Csdn博客 矩阵乘积的行列式等于行列式的乘积证明



基礎数学演習i




Ppt 第二章行列式 Determinant Powerpoint Presentation Free Download Id



Mathematics For Engineering Iii




4 4 随伴行列 考える線形代数 Wiki Atwiki アットウィキ



基礎数学演習i




行列式证明二次曲线定点 值 问题 每日头条




固有値についても証明問題を解いてみました あってますか 何か他の解き方はありますか Clear




线性代数 行列式 单元综合练习题及参考解答 网易订阅




3次正方行列の逆行列 その求め方 身勝手な主張



行列式の証明問題について 解答を教えてください Anの行列式 Yahoo 知恵袋



行列式解幾何題舉例 從初等數學到高等數學 Zi 字媒體




克莱姆公式 克莱姆法则例题 行列式克莱姆




行列式函数问题 知乎




三角形行列式计算证明 见下图 有关反上三角行列式的证明问题 三人行教育网 Www 3rxing Org




行列式函数问题 知乎



线性代数难题来大神求解 信息图文欣赏 信息村 K0w0m Com



线代随笔16 正定矩阵及相关性质




第二章行列式第一节二阶 三阶行列式 Ppt Download



范德蒙行列式例题请教一个范德蒙的问题




行列の証明問題を解きました あってるでしょうか Clear




2次行列と証明問題




线性代数行列式问题x1为什么是d1 D 这是为什么这也算求证明或者说清楚道理 雨露学习互助



独特角度证明行列式的有关性质 代数




上三角行列式证明 技术成就梦想 梦想成就未来 Csdn博客 上三角行列式




Edmonds Edmonds 1967 7 8 Edmonds Ivanyosqiaosubrahmanyam 15



Http Storage Xuetangx Com Public Assets Moocap Attachment Pdf




正則行列 逆行列 公式と性質 証明付 理数アラカルト




行列式多项式的根的问题怎么算 证明下面行列式等于1的n次本原根多项式相乘的形式 三人行教育网 Www 3rxing Org




どのような事を示せば証明出来るのかが分かりません 証明問題の時の思考回路も教えて頂け Clear



矩阵 范德蒙德行列式 Arcobaleno 程序员宅基地 范德蒙德行列式 程序员宅基地




行列式性质证明题 证明题行列式 三人行教育网 Www 3rxing Org




大きい行列の問題




1 の誘導の乗り方がわからなくて 2 の行列式の値が求められません Clear




中值定理证明题中的 行列式问题 百度经验



User Math Kyushu U Ac Jp Plugin Attach Refer Ochiai 2flaex1 Openfile Laex2solution 28ver0523 29 Pdf




行列が正則であることの同値な条件と証明 高校数学の美しい物語




行列式乘法规则的证明方法及其应用 豆知网



复旦大学 高等代数 每周一题关于伴随矩阵和多项式的一个小问题 哔哩哔哩 つロ干杯 Bilibili



0 件のコメント:
コメントを投稿